Stand-by

Now loading "Examples of Characterization-II" page

from www.marcelpatek.com ..... please wait.

1. Examples of a Display Characterization - continues:

[1B]-Linearization and matrix optimization :

In this section we will explore several model-based approaches commonly used to characterize a calibrated state of computer monitors. These models describe the physical process by which the output device renders colors. A primary advantage of the model-based approaches is that they require fewer measurements than methods based on icc profiles. Such models usually include some combination of the power-law mapping (linearization), [3x3] or [3x4] matrix conversion, and the white point normalization.

Models for Display Characterization:

Let's evaluate common linearization models and see how well they describe the Eizo CG19 LCD display. Table 4 summarizes conversion matrices and linearization models used in these examples. Most of the presented methods are included in the Excel file (Ramps_XYZ.xls). More advanced methods use the Matlab code in form of the .m files.

Table 4 . Processing and linearization parameters for display characterization.
ID Matrix type Excel sheet Linearization model Filename (Excel; Matlab)
1. [3x3]+blk; mon white sheet XYZ;run [A] sRGB model Ramps_XYZ.xls; main.m
2. [3x3]+blk; D50 sheet XYZp; run custom [G] rgb = dc^g (simple gamma) Ramps_XYZ.xls; main_simple_gamma.m
3. (opt. [3x3])+blk; D50 sheet XYZp; run [H] via inv(MD50) (eq. XIII) Ramps_XYZ.xls; optT_lininv2D50.m
4. [3x3]+blk; D50 sheet XYZp; run [C] sRGB encoding standard using norm. XYZ data Ramps_XYZ.xls; Kang_custom_rgb_v2.m
5. [3x3]+blk; D50 sheet XYZp; run [A] sRGB encoding standard on optim. linRGB+coeff NA; main_optim.m
6. full 3x4 optim; D50 sheet XYZp; run [C] optimized LUT NA; loop1_D50.m+loop2_D50.m

Notes on abbreviations used in Table 4 .

  1. Model builds the [3x3] matrix (eq. VI) derived from the display primaries that are adapted to the current monitor white point. This [3x3] matrix is then extended to [3x4] matrix by including the XYZ values of the black level. Linearization of R'G'B' values uses the standard sRGB gamma encoding formula (eq. 1.7a, 1.7b). In the pseudo code: {if rgb(n) <= 0.03928 then rgb(i) = rgb(n)/12.92; else rgb(i) = ((rgb(n)+0.055)/1.055)^2.4}. Calculated tristimulus values XYZ are then chromatically adapted to D50 source using the Bradford transform and finally converted to Lab(50) values. The overall process of generating the "theoretical" L*a*b* values for the displayed ramps is following: R'G'B'->[linearization]->RGB->[3x3]->XYZ(mw)->[Bradford]->XYZ(D50)->L*a*b* (mw - monitor white). This is very straightforward process which can be "automated" in the Excel spreadsheet.
  2. Similarly to (1), this model builds the [3x3] matrix (eq. VI) derived from the display primaries - in this case first transformed to D50 source using the Bradford CAT. The [3x3] matrix coefficients are then scaled to the D50 white point (white point adapted). White point adapted [3x3] matrix is extended to 3x4 matrix by including the XYZ values for the black level. Linearization of RGB (dc) values uses a simple gamma model: {rgb = dc^γ}. Calculated tristimulus values XYZ(D50) are then converted to Lab(50) values. In brief, there are two differences from the method 1: first, the transfer matrix contains D50 transformed data, and second, linearization uses simple "power-law gamma" instead of the sRGB encoding.
  3. Only Matlab code is used for the [3x3] matrix (eq. VI) optimization; then the Excel sheet is used for further processing (optional). For linearization, this model builds the [3x3] matrix derived from the display primaries (3) first transformed to D50 source (1->2) and scaled to the D50 white point (4). Black levels are subtracted from [3x3] coefficients. Inverse matrix (5) is calculated with XYZ values for the blacks included. Overall, linearized RGB values (7) are calculated by inverting the transfer matrix as in eq. XIII (Figure 9.). These values are then used in the classical RGB->XYZ matrix transformation (eq. VI) to obtain the "theoretical" XYZ values for the comparison with the measured ones. Algorithm minimizes the difference between measured and predicted L*a*b* values by changing the [3x3] part of the RGB->XYZ matrix. Each optimization of the [3x3] matrix is then followed by extension to [3x4] matrix by including XYZ values for the black (eq. XIII). The white point adaptation to D50 illuminant is also performed. Overall, the linearization is constant while the [3x3] part of the [3x4] conversion matrix is optimized.
    Figure 9: Linearization model using matrix inversion and correction for the black levels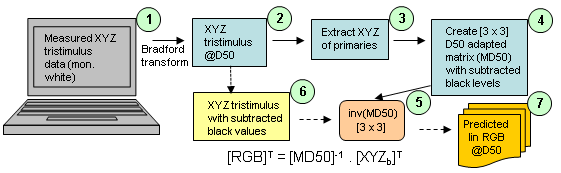
    linearization scheme
  4. Model uses the [3x3] matrix (eq. VI) derived from the display primaries first transformed to D50 source and adapted to the D50 white point. XYZ values for the black are subtracted from measured XYZ values and the resulting "black"- corrected values are normalized. These and normalized R'G'B'(n) values are then used in a non-linear curve fitting to determine (b) and (γ) coefficients (eq. V). Coefficients obtained from the non-linear fitting are then used to calculate linearized RGB values which are used next to predict XYZcalc values. The [3x3] matrix is extended to 3x4 matrix by including XYZ values for the black (eq. XIII). This matrix is not optimized. The corresponding L*a*b* values are then compared with L*a*b* values of the measured patches. Again, coefficients (b) and (γ) have to be calculated using any standard nonlinear curve fitting program and then entered into the Excel sheet XYZp (cells K17:M18). This scenario corresponds to the example described in "Principles of Color Technology" (R.S. Berns), pp. 168-169.
  5. Only Matlab code. Model uses the [3x3] matrix (eq. VI) derived from the display primaries first transformed to D50 illuminant and scaled to the D50 white point. No prior linearized values are needed. RGB encoding standard linearization model is used as part of the 'fminsearch' algorithm to find the best (b) and (γ) coefficients (eq. V) by minimizing the difference between measured and predicted L*a*b* values (and thus the best linear RGB). Optimization is done for each channel independently. This approach adapts coefficients of the RGB standard encoding model (similar to GOG) to provide the optimum linearization while the conversion [3x3] matrix (extended to 3x4 matrix by including XYZ values for the black) is not optimized.
  6. Only Matlab code. This is the most elaborate algorithm based on the work of Berns. Complete flowchart is shown in Figure 10. Briefly, the algorithm iteratively optimizes the full [3x4] matrix by minimizing the difference between measured and predicted CIELAB values. Resulting [3x4] matrix is D50 adapted. New linear RGB values are predicted after each step.

    Since both the matrix coefficients and the linearized RGB values are optimized, there is no way to tell what values are actually sent to the monitor. Thus this optimization only reveals weak spots in the characterization/calibration results. Watch for high DE2000 and sigma values as well as for DE2000 spikes in measured ramps, patches, and gray-scale.

    Full description is given next.
Figure 10: Measurement, calculation, and optimization flowchart
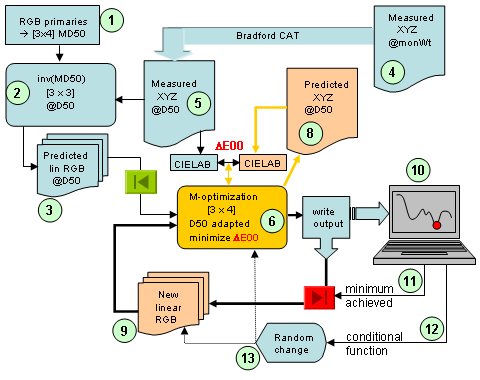Opt_scheme

Measured (experimental) tristimulus values of each primary ramp (4) are first transformed to D50 illuminant using the Bradford chromatic adaptation transform (5). Next, the [3x3] matrix derived from measured display primaries is extracted, scaled to the D50 white point, and expanded to [3x4] matrix by including the experimental XYZ values for black level (1, 5). The [3x3] portion of this matrix is inverted and corrected to account for non zero radiant output at the black level(2). Exact math description is shown in eq. (XIII). Using the equation XIII together with the XYZ values from (5) and the inverted matrix (2), radiometric scalars (linearized RGB values) are calculated as the initial values for optimization (3) (same as in Fig. 9). Optionally, one can just use the sRGB linearized values as the first guess. Using multi-dimensional nonlinear optimization algorithm (fminsearch in Matlab), the coefficients of the [3x4] matrix (6) are optimized until the average CIEDE2000 color difference between measured (5) and estimated (8) tristimulus values for all three ramps is minimized. Optimization of the [3x4] matrix has additional condition that minimizes the difference between predicted white point and the standard D50 illuminant (white point adaptation). After each optimization of the [3x4] matrix, new linear RGB values (9) are calculated using eq. (XIII). Graphical output of the optimization is displayed on screen (10) for a visual inspection and convergence. Since the chosen optimizer can be "trapped" in a local minimum, two random functions (13) are included to alter the predicted linear RGB values (9) and the [3x4] matrix coefficients (6) under certain conditions (11,12). This feature allows for multiple sampling of the scanned hypersurface. Matlab code for the above described optimization including all the dependent files can be freely obtained (send me an e-mail at marcel@marcelpatek.com).

(top)↑
Ramps:
Table 5 . Results of Eizo CG19 characterization - ramps.
ID Channel Ave DE2000 Sigma DE2000 Max DE2000
1. RGB 0.39 0.24 1.72
1. R 0.25 0.17 0.83
1. G 0.42 0.31 1.72
1. B 0.51 0.15 1.06
2. RGB 0.77 0.81 4.41
2. R 0.78 0.90 3.68
2. G 0.85 0.99 4.41
2. B 0.74 0.49 2.43
3. RGB 0.10 0.10 0.91
3. R 0.08 0.05 0.31
3. G 0.11 0.05 0.28
3. B 0.12 0.15 0.91
4. RGB 0.28 0.21 1.19
4. R 0.22 0.19 0.87
4. G 0.23 0.24 1.19
4. B 0.39 0.16 1.03
5. RGB 0.31 0.26 1.48
5. R 0.26 0.24 1.17
5. G 0.25 0.32 1.48
5. B 0.43 0.13 0.91
6a. RGB 0.11 0.08 0.77
6a. R 0.08 0.04 0.22
6a. G 0.14 0.04 0.22
6a. B 0.10 0.12 0.77
6b. RGB 0.09 0.08 0.73
6b. R 0.10 0.05 0.28
6b. G 0.06 0.03 0.17
6b. B 0.10 0.11 0.73

Now, we will apply all six methods to analysis of RGB ramps. Inspection of the data in Table 5 clearly shows that simple gamma model performs quite poorly (ID 2). On the other hand, the full matrix and RGB optimization as outlined in Figure 10 provide the best results ID (6a, 6b). Entries 6a and 6b are just different minima selected from the 114-itteration run (Figure 11 ).

While method 1 performs reasonably well, models based on parametric linearization (3-5) have a slight edge over the sRGB linearization. Method 3 might be the best choice from these as the overall descriptor statistics is very good. Another way to look at the results would be from the perspective of available software. If one prefers to stay with the Excel and some on-line Java based nonlinear curve fitting programs, then methods 1 or 4 are the best choices. I would recommend method 1, since it is easy to implement.

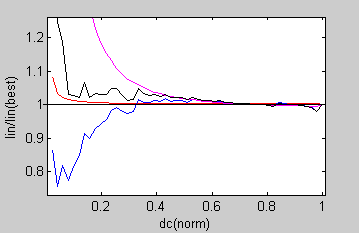
More detailed analysis of the data suggests (not surprisingly) that performance of the model depends mainly on two variables: quality of the linearized RGB values and the transfer matrix. To compare linear RGB values used in, or coming from different methods, the ratio of linearized RGB values and the "best" linear values (6b) was calculated (Figure 12 ). Red line corresponds to linearization that was achieved by inverting the transfer matrix followed by multiplication with the measured (black corrected) tristimulus data as per eq. XIII. The blue line is result of non-linear curve fitting using RGB encoding standard as described in method (4).

Figure 11:

optimMatrix and LUT optimization: Snapshot of 114-step run.

Magenta line represents just the normalized tristimulus data. Finally, the black line corresponds to sRGB gamma coding. Ideally, the line should be as close to the 1 as possible. Qualitatively, lines in Fig. 12 reflect the same order of method performance as discussed above (lin via inv > sRGB > std RGB encoding with fitted coeff. > normalized XYZ). Just a note, Fig. 12 described only the X-component of the XYZ triplet for the red channel.

Figure 12: Ratios of OETF/OETF(6b)
Kang_custom_rgb_v2web.m

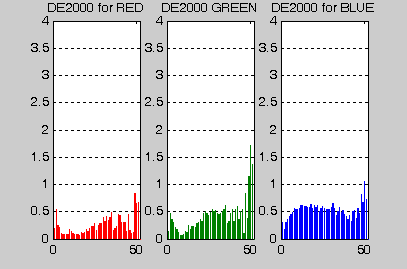
To get better appreciation of the statistical values, Figures 13, 14 show the CIEDE2000 errors for each channel when method (1) and (6) are used, respectively. From the CIEDE2000 ramp profiles, one can clearly see the benefit of full matrix and LUT optimization. Values close to 50 at the x-axis correspond to dark parts of the ramp. Interestingly, while the red and green channels have apparent valleys in the bright regions (Fig. 13 ), the blue channel has a broad "shoulder" that is still apparent in the fully optimized system (Fig. 14 ). Red and green channels are nicely optimized while the blue channel has some intrinsic problems. However, note that none of the methods would produce noticeable differences in colors (CIEDE2000 < 1 for most of the brighter areas).

Figure 13: Results of RGB to XYZ conversion: Method 1
main.m

 

Figure 14: Results of RGB to XYZ conversion: method 6
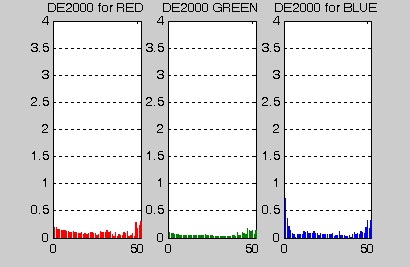XYZ2LAb_3x4_main.m

(top)↑
Patches:
Table 6 . Results of Eizo CG19 characterization - Patches.
ID Channel Ave DE2000 Sigma DE2000 Max DE2000
1. RGB 0.40 0.22 1.17
1. Gray 0.65 0.30 1.17
1. RGBCMY 0.18 0.04 0.22
1. Colors 0.34 0.14 0.71
3. RGB 0.41 0.22 1.17
3. Gray 0.65 0.30 1.17
3. RGBCMY 0.27 0.09 0.41
3. Colors 0.35 0.15 0.74
6. RGB 0.17 0.22 1.47
6. Gray 0.08 0.13 0.74
6. Colors 0.17 0.19 1.47

Methods used for analysis of patches and gray-scale images differ slightly from the previously discussed models that were used for the analysis of ramps. The reason is that we no longer have the XYZ data available for every 5 steps of primaries in each RGB channel. While one can certainly build a look-up table for each channel and then predict any displayed color, this approach has some practical limitations. Besides being computationally intensive, the white points and even the tristimulus data for the RGB primaries vary slightly from the measurements of ramps and other color patches. It is not unusual that monitor white point (and color temperature) changes slightly even during one measurement run. To adequately analyze the data obtained from color patches and gray-scale ramps, we will use the standard sRGB gamma encoding formula as described above (method 1). Conveniently, calculations can then be performed in a spreadsheet. We will also use the method 3, which keeps the linearization constant while the [3x3] part of the [3x4] conversion matrix is optimized. Thus abbreviations used in Table 6 follow the same notation as described earlier. For method 3, we have two possibilities. Linearization in (3) uses the standard sRGB encoding while in the 3a, the linearization is done by inverting the [3x3] transfer matrix (eq. XIII).

Now back to the analysis. Similarly to the tables discussed earlier, Table 6 summarized the average CIEDE200 color difference, standard deviation of DE2000 (sigma), and the maximum DE2000 in patches containing 31 gray steps, six primary and secondary colors (RGBCMY), and 122 color patches. Data in Table 6 clearly shows that optimization of the [3x3] portion of the [3x4] transformation matrix does not improve the overall statistics (1 vs. 3). This would indicate that optimization based on

Figure 15: Method 1 - DE00 for color patches
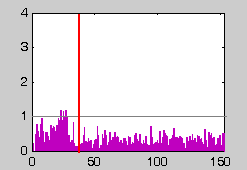Calib_eval\Patches

sRGB-linearized data is not finding any better coefficients. In comparison with the LUT-based icc profile method, here the gray-scale seems to be slightly worse while color patches are about the same. This can be seen after comparing Figures 15 and 7. Again, bars left of the red vertical line are the gray steps, bars to the right are the color patches. Black horizontal line indicates the threshold value of 1 for the DE2000 (JND). The same conclusions can be better appreciated from Figure 16. In comparison to Figure 6, the gray ramp has indeed greater color differences. The color patches are about the same. DE2000 greater than 0.5 is indicated by a yellow rectangle while the DE2000 > 1.0 is in red rectangle. These data would also suggest that the LUT-based icc method benefits from "improved" look-up tables that brought a "correction" to the gray scale during profiling. Examples shown in this section come from directly from measurements off the screen.

Figure 16: Method 1 - DE2000 for color patches
patches_1

When inverted XYZ data are used for the RGB linearization, the results look much better (Table 6 / 3a). Theoretically, without any changes in the [3x4] matrix the color differences should be zero as the linearized data are the same as the measured XYZ data (XYZ->RGB->XYZ). However, due to the matrix optimization, non-linear irregularities in patches and gray-scale will become quickly apparent (Figure 17). It is mostly the blue region where the largest color differences are noticeable. This observation has been made earlier (Table 5) suggesting some underlying weakness in the blue channel. Color differences are calculated from L*a*b* values measured vs. predicted "reference' L*a*b* values.

For a comparison, computationally intensive Method 6 with the full optimization of [3x4] matrix and linear RGB values was run. Inspection of the Table 6 reveals that, as expected, the main statistical parameters changed dramatically. However, as the gray-scale part improved significantly, some of the colors could not be optimized. This resulted in visible remaining spikes in the DE2000 vs. RGB plot (compare Fig. 18 and 19).

Figure 17: Method 3a - DE2000 for color patches
patches_3a

Colors of the "non optimizable" peaks are indicated in the Figure 17 (panel 2). Not surprisingly, we see some blue colors and some red - orange colors. Interestingly, these higher DE2000 spikes can be spotted in the non-optimized Method 1 (Figure 18, right panel). These results support the use of Method 1 for a quick analysis of monitor calibrations.

In summary, the model-based methods perform quite well for color patches. There are greater color differences predicted for the gray-scale ramps than when icc profiles are used. It still may be faster to use icc profiles for the "reference" data, but more information can be obtained from analysis of direct screen readings. Simple sRGB encoding standard for R'G'B' linearization was found to be adequate and it is implemented in the spreadsheet Patches_XYZ.xls.

Figure 18: Method 1 - DE00 for color patches
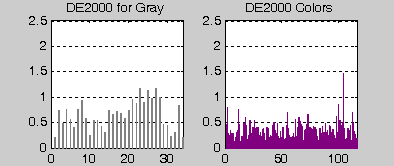Custom_lin_3x4_ptch.m
Figure 19: Method 6 - DE00 for color patches - Optimized
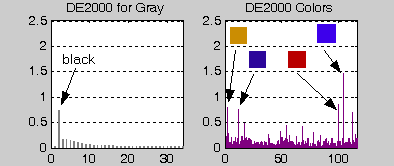calculations\analyze

 

(top)↑
Gray ramps:
Table 7 . Results of Eizo CG19 characterization - Gray ramp.
ID Channel Ave DE2000 Sigma DE2000 Max DE2000
1. RGB 1.26 0.55 2.81
1. Gray 1.37 0.45 2.81
1. RGBCMY 0.24 0.14 0.40
3. RGB 1.28 0.50 2.81
3. Gray 1.37 0.45 2.81
3. RGBCMY 0.51 0.20 0.85
3a. RGB 0.04 0.11 0.62
3a. Gray 0.02 0.09 0.62
3a. RGBCMY 0.18 0.14 0.40

The same methods as for analysis of color patches were used for analysis of gray-scale ramps. Again, the standard RGB encoding was used for R'G'B' linearization (Table 7 / 1, 3). Method 3a is described in the preceding paragraph. Input data used in this section are same as the data used in the LUT-based example.

First, the 51 ramps in steps of 5 were run on the screen and their tristimulus data (XYZ) were measured by the X-Rite colorimeter DTP-94. Additional white, black, and RGBCMY patches were added to account for black levels and the white point. Measured tristimulus data were converted to D50 source (Bradford transform Dmw->D50) and used for further analysis (mw stands for "monitor white").

Figure 20 shows the distribution of DE2000 color difference values along the whole range of R'G'B' values (0 is black, 51 is white). Data was generated using the Method 1 (Table 7). Profile of the gray ramps is relatively similar to the LUT-based results (Figure 7). Particularly the dark areas (on the left0 match quite well. The LAB a*,b* profile (Figure 21) is nearly identical to the LUT-based results (Figure 8) indicating that increase in the b* component cannot be compensated by the larger LUT-based profile. Overall, while the gray-scale looked smooth on the screen, darker areas suffer from a blue shift and thus higher color difference. The monitor gamma and color temperature were as expected.

Figure 20: Method 1 - DE00 for gray patches
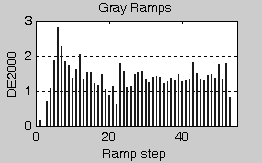RGB_icc_Lab_gray.m
Figure 21: LAB (a*,b*) profile of the gray patches
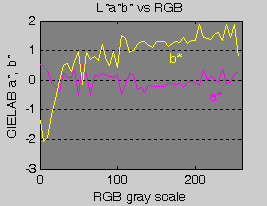disp_g-ab

In conclusion, several methods were presented for display characterization. Most of the input data as well as the processing spreadsheets can be downloaded from this section. For a quick assessment of the display profile, the standard RGB encoding can be used for linearization of the input values (R'G'B'). The necessary transfer matrix can be assembled from XYZ values of the RGB primaries.

Run your own characterization of monitor calibration:

This is a compact description of steps for characterization of monitor calibration. These steps work on Windows systems calibrated by any of the above mentioned methods. Specifically, I use the Argyll CMS utilities targeted to provide srgb response curve and the overall gamma of 2.2. We will use either a colorimeter or spectrophotometer Eye1 Pro. Remember to let the monitor stabilize for about 30-60 min. Make sure that calibration file is loaded into the video card LUT.

  1. Download LOGO and .ti1 formatted files for RGB ramps, color patches and gray patches.
  2. Unzip the file and place the content into appropriate directories. Place PM5 LOGO files into C:\Program Files\GretagMacbeth\ProfileMaker Professional 5.0.8\Reference Files\Monitor; Argyll .ti1 file into c:\cms\bin\data (depends where the Argyll is installed).
  3. Depending on software you plan to use for measurements, connect the measuring device to a USB port of your computer and launch the chosen software (PM5, Argyll).
  4. Measure the patches and in the case of PM5 save the output file.
  5. To process the data, download all three Excel workbooks. Import (paste/enter) the acquired data into the sheet "data_in". Once the data is there, XYZ components are normalized and are automatically copied into the main tab "process". Follow the instructions in each workbook.
  6. In the "Process" sheet, click the "1. Clear" macro button in the sheet to clear the old data.
  7. Click the "2. Convert to D50" macro button to convert the XYZ data recorded at the monitor white point to th D50 illuminant. The corresponding L*a*b* (D50) data is also calculated.
  8. Click the macro button 3. (next to [A] in a green field) to send the R'G'B' data through the linearization, matrix conversion, Bradford transform, and Lab calculations. All the steps are automatically performed at once.
  9. Click the "4. Calc DE2000" macro button to calculate the color difference and other colorimetric and statistical parameters.
  10. Optionally, there are three or more of other tabs useful for further analysis. The "Analysis" tab combines all the data into one area. One can plot the data in a graphical form. Tag "Gray" shows log-log gamma fit and L*a*b* plot along the whole luminance range. The other two tabs - "LOGO_Lab" and "LOGO_GM50" are formatted to output the specific LOGO format for further analysis in the ColorThink Pro or the PatchTool. Just click the macro button on the respective tab. Files are created in the same directory as the main worksheet.

 



back to Part 1

Last update : September , 2008

Back to TOP